GCN最近两三年特别火，这篇article主要总结GCN这个模型的发展历程。

论文1：SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS -- Kipf（ICLR 2016）

\(Z=f(X, A)=\operatorname{softmax}\left(\hat{A} \operatorname{ReLU}\left(\hat{A} X W^{(0)}\right) W^{(1)}\right)\)

\(\hat{A}=\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}}\)

采用了两层传播。

Kipf的这篇工作针对的是图半监督学习的节点标签分类问题。图就是普通的单一无向关系图(比如朋友圈)，半监督学习就是在给定部分节点标签下，学习到所有节点的标签。因此这个模型的特点是：

1. 没有考虑到图中可能存在的多种关系。
2. 任务是针对节点分类node classification问题。

论文2：Inductive Representation Learning on Large Graphs -- Hamilton （NIP2017）也就是GraphSAGE

Loss function:

\(J_{\mathcal{G}}\left(\mathbf{z}_{u}\right)=-\log \left(\sigma\left(\mathbf{z}_{u}^{\top} \mathbf{z}_{v}\right)\right)-Q \cdot \mathbb{E}_{v_{n} \sim P_{n}(v)} \log \left(\sigma\left(-\mathbf{z}_{u}^{\top} \mathbf{z}_{v_{n}}\right)\right)\)

这篇文章的要点：

1. 也是针对的单一无向图，所以没有考虑和学习边
2. 提出了aggregator的概念

对GCN的突破点是，实现了inductive化。

论文3：Modeling Relational Data with Graph Convolutional Networks -- Schlichtkrull (2017) 也就是R-GCN

\(h_{i}^{(l+1)}=\sigma\left(\sum_{r \in \mathcal{R}} \sum_{j \in \mathcal{N}_{i}^{r}} \frac{1}{c_{i, r}} W_{r}^{(l)} h_{j}^{(l)}+W_{0}^{(l)} h_{i}^{(l)}\right)\)

要点：适应了KG特性：不同的关系的W不同，即考虑了关系的特殊性。

论文4：End-to-end Structure-Aware Convolutional Networksfor Knowledge Base Completion -- Shang （aaai 2017） Weighted GCN

相比于kipf的经典GCN，这个weighted GCN为每一层的每个关系单独学习一个权重。

\(h_{i}^{l+1}=\sigma\left(\sum_{j \in \mathbf{N}_{\mathbf{i}}} \alpha_{t}^{l} h_{j}^{l} W^{l}+h_{i}^{l} W^{l}\right)\)

要点：这里的权重仅仅是一个数，而不是向量。因此和R-GCN不同。

论文五：COMPOSITION-BASED MULTI-RELATIONAL GRAPH CONVOLUTIONAL NETWORKS -- Vashishth （ICLR 2020）

提出了一个general的KG上的GCN模型。

\(\boldsymbol{h}_{v}=f\left(\sum_{(u, r) \in \mathcal{N}(v)} \boldsymbol{W}_{\lambda(r)} \phi\left(\boldsymbol{x}_{u}, \boldsymbol{z}_{r}\right)\right)\)

其中的W有三种：

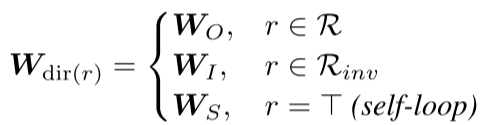
可见weight不是relation-specific，而是type-specific的。