This paper did a detailed survey on Representation Learning on (Knowledge) Graph. It gives a valid devolopment progress on static KGRL and makes a summary on approaches of Dynamic Graph Representation Learning. They describes existing models from an encode-decode perspective and categorize these encoders and decoders based on the techniques they employ.

And in the end they highlighr directions for future research.

Firtly I want present the devolope line of KGRL. (Understanding big picture of KGRL is very necessary!!)

In this section I present several definations:

Dynamic Graph (Not KG):

1. Continuous-time dynamic graph (\(CTDG\)): \(CTDG = (G,O)\), \(G\) representes graph at time \(t_1\), \(O\) represents several observations occur after \(t_1\). This defination of dynamic graph can capture all the changes happened over time.
2. Discrete-time dynamic graph (\(DTDG\)): \(DTDG = (G_1, G_2, ..., G_n)\). Each \(G_i\) is a snapshot and representes graph at time \(i\). \(DTDG\) may not capture all the changes on a graph because there may be a time interval between two adjacent snapshots.

We call both \(CTDG\) and \(DTDG\) dynamic graph. Most existing models for dynamic learning is on \(DTDG\) because it is easier.

KGs: I think I am a bit of familiar with.

General Tasks for Dynamic graphs:

1. Node classification
2. Graph complement/Link prediction: main task of KGs
3. Graph classification

Streaming scenario: A model may not have enough time to retrain compeletly or in part when new observations arrive. Streaming scernarios are often best handled by \(CTDGs\).

Encoder-decoder framework for static graph and KGs:

Decoders for static graph: very simple

1. average of two vectors
2. element-wise multiplication of two vectors
3. element-wise absolute value of the difference of the two vectors
4. elemet-wise squared value of the difference of the two vectors

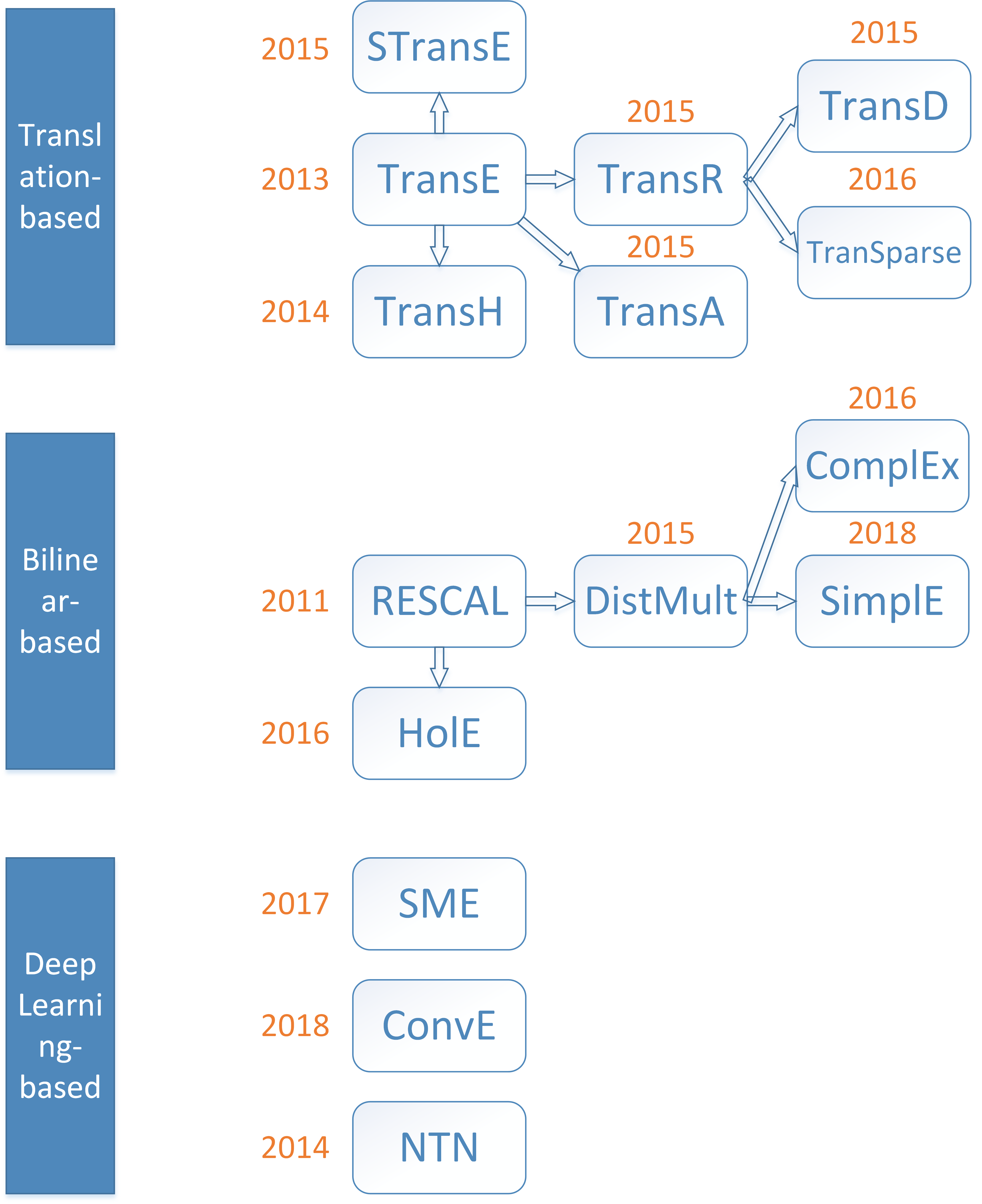
Decoders for static KGs: much more complex. Examples of each catelogue is shown in previous picture.

1. Translation-based models
2. Bilinearity-based models
3. Neural network-based models 

Encoders for static graph:

1. High-Order Proximity Matrices: an extension of adjacency matrices
2. Shallow Encoders
3. Decomposition Approaches: its idea is that connected nodes are close to each other in the embedded space.
4. Random Walk Approaches
5. Autoencoder Approades:
6. GCN Approaches

Encoders for static KGs: very few compared to static graph

1. shallow encoders
2. GCNs: such as R-GCN

Encoder-decoder framework for dynamic graph: (Note that no Encoders and Decoders of dynamic KGs are introduced in this survey paper).

Decoders for dynamic graph: I know nearly nothing about this.

1. Time -predicting decoders
2. Time-conditioned decoders
3. Staleness

Encoders for dynamic graph:

1. Aggregating Temporal Observations
2. Aggregating Static Features
3. Time as a Regularizer
4. Decomposition-based Encoders
5. Random Walk Encoders
6. Sequence-Model Encoders
7. Autoencoder-based Encoders

Applications, Datasets and Codes

Applications:

1. Link prediction
2. Entity/relation prediction
3. Recommender Systems
4. Time Prediction
5. Node classfication
6. Graph classification
7. Network clustering
8. Question/query answering

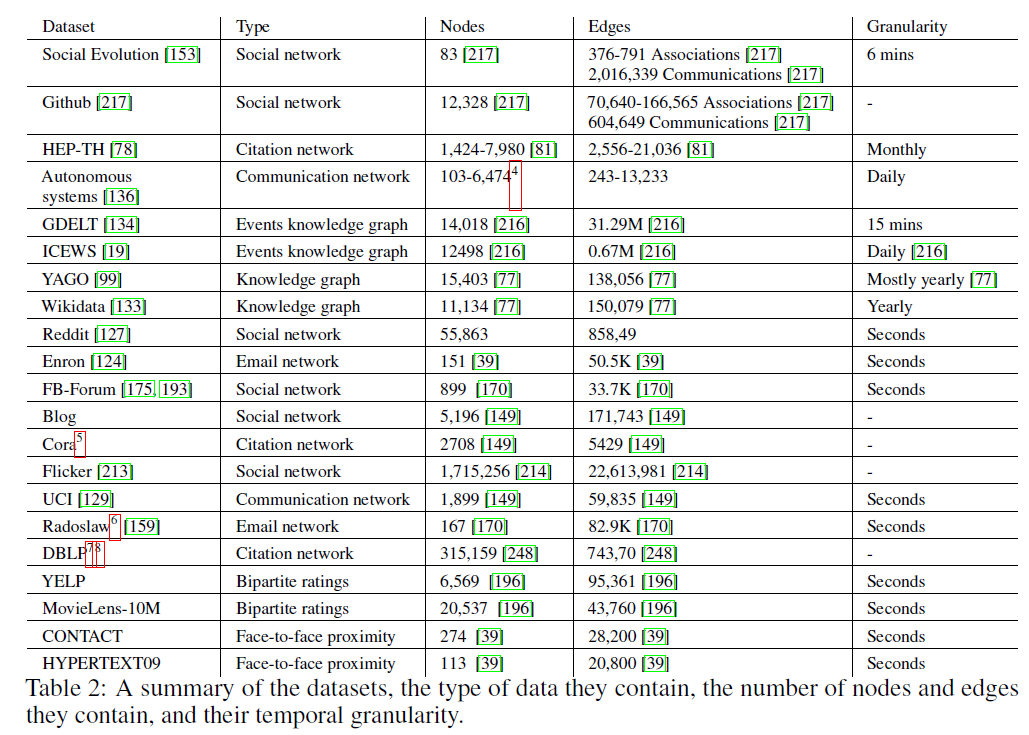
Datasets: A collection of datasets used for research on static and dynamic graphs. 

Future Direction:

1. The best way to extend the existing models for daynamic graph to KGs is still not clear! 
2. Currently representation learning algorithms have been mostly designed for \(DTDG\), with only few works on \(CTDG\).