这篇文章发表在2019年的ICLR上

主要思想：将 \(h\)，\(r\), \(t\) 用复数来表示，即 \(h\), \(t\), \(r\) \(\in\) \(C\)。

首先，任何复数 \(Z\) 可表示成： \(Z = r(\cos \theta+i \sin \theta) = r \cos \theta + ir \sin \theta\)

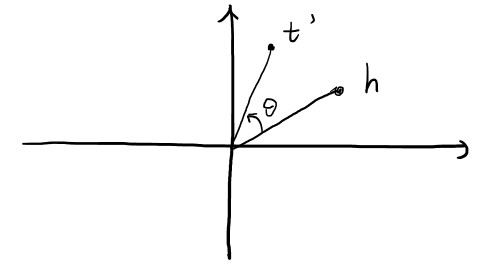
在RotatE中，约束 \(|r| = 1\)，这样 \(r\) 可看作是一种旋转，譬如

\(h \circ r=h(\cos \theta+i \sin \theta)=t^{\prime}\), 这里的 \(\circ\) 是 element-wide product。

distance function:

\(d_{r}(h, t)=\left\|h \circ r-1\right\|\)

Loss function:

\(L=-\log \sigma\left(\gamma-d_{r}(\mathbf{h}, \mathbf{t})\right)-\sum_{i=1}^{n} \frac{1}{k} \log \sigma\left(d_{r}\left(\mathbf{h}_{i}^{\prime}, \mathbf{t}_{i}^{\prime}\right)-\gamma\right)\)

其中 \(d_{r}(\mathbf{h}, \mathbf{t})\) 是 negative sample。

RotatE 可以很好的 model 几乎所有关系：

Three types of relation:

1. symmetric / antisymmetry eg. \(\left(h_{1}, r, h_{2}\right) \Leftrightarrow\left(h_{2}, r, h_{1}\right)\)
2. inversion e.g. \(\left(h_{1}, r_{1}, h_{2}\right) \Leftrightarrow\left(h_{2}, r_{2}, h_{1}\right)\)
3. composition e.g. \(\left(h_{1}, r_{1}, h_{2}\right) \wedge\left(h_{2}, r_{2}, h_{3}\right) \Rightarrow\left(h_{1}, r_{3}, h_{3}\right)\)

最后除了普通的Link prediction实验外，还进行了contry dataset的实验。